What is the Monte Carlo code MCSHAPE?

When x-rays penetrate in the matter, they interact with the atoms, producing secondary radiation that carries important information about the composition of the target. The polarization state is one of the properties of the incoming photons which changes as a consequence of the number and the type of the undergone interaction. Therefore, to study properly the atomic properties of a material, it is necessary to consider the evolution of the polarization state of radiation. MCSHAPE is a Monte Carlo code developed to describe the evolution of the polarization state of x-ray photons as a consequence of the multiple scattering collisions undergone during the diffusion into the sample. In order to study properly the transport of photons with an arbitrary state of polarization, the model adopted in this code is derived from the so called ‘vector’ transport equation. Using the Stokes parameters I, Q, U, and V, having the dimension of an intensity and containing all the physical information about the polarization state, MCSHAPE simulates the full state of polarization of the photons at any given position, wavelength and solid angle.

OUTLINE OF THE CODE

History

The Monte Carlo code MCSHAPE was born in 1995, starting from a scalar (deterministic) code called SHAPE. The first version of the code was written in Pascal and performed analog calculation of, at least, four collisions of the photons in the matter. Then, two new codes was developed using FORTRAN:

• MCSHAPE0, that follows up to four collisions of the photons in the target, using analog calculation
• MCSHAPE1, in which there is no limit in the number of the collisions considered

 The common structure of the two Monte Carlo codes is presented in fig. 1.

Fig. 1 - Structure of the code.

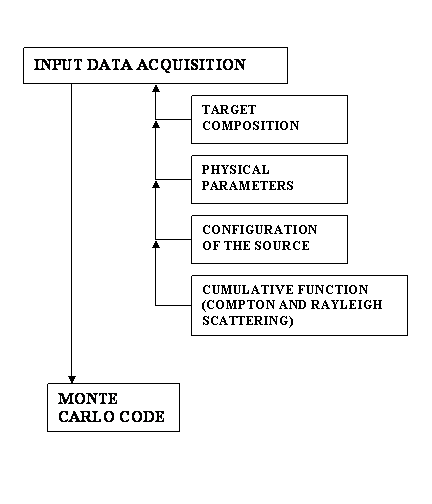
The Monte Carlo codes follow the histories of the photons until the absorption in the sample or their arrival to the detector. The physical model adopted allow to consider:

• source with arbitrary state of polarization
• homogeneous targets made of different elements, with finite thickness
• monochromatic and polychromatic sources
• Doppler broadening on Compton scattering 

The authors of the codes have dedicated great attention at the libraries of the physical parameters involved in the simulation (coefficients of attenuation, form factors, cross sections, and so on).

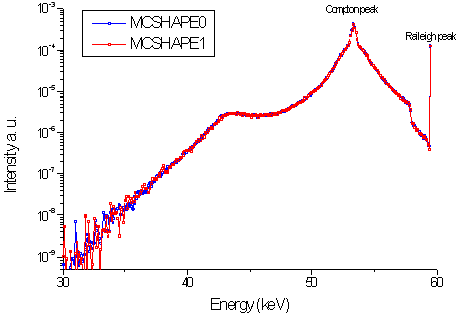
Fig. 2- Benchmarking MCSHAPE0 and MCSHAPE1. The target is aluminum, the source is unpolarized and the scattering angle is 90º. Both codes perform four collisions. The similarity of both results ensures the proper answer of the N-collision

Geometry of the scattering

The model adopted in the code MCSHAPE assumes that photons interact only within the target, i.e. those photons escaping towards the surrounding empty space or air may suffer absorption but never return back to the target. In fact, this is a good model to represent the behaviour of radiation in two media of different density, the one in the sample being much greater than the density in the half-space outside the target. The geometry of MCSHAPE backscattering model is shown in fig. 3.

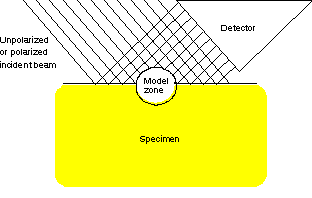
Fig. 3 – Geometry of the backscattering model used by MCSHAPE.

Selection of the scattering angle for Rayleigh and Compton scattering

For the selection of the scattering angle, the code operates as follows: the scattering angle is generated randomly thanks to the phase function of the collision considered in the center of mass reference system; then, the outgoing direction is converted in the laboratory reference system.

It is important to underline that, in the polarization model adopted in the code MCSHAPE, the collision term in the vector transport equation is described by a matrix kernel. So, in the code, for the selection of the scattering angle, a mixed method is used: for every collision, the final polar angle is sampled from the scalar differential cross-section for the event (isotropic for the photoelectric effect, anisotropic for Compton and Rayleigh scattering). The cosine of the scattering angle is determined thanks to a cumulative function built starting from the same distributive function which is used in the scalar representation of the scattering kernel. As a consequence, only the first component of the Stokes vector, the intensity I, is optimized, while the other components Q, U and V are computed using weights.

The azimuthal angle in the local center of mass reference system is sampled uniformly.

©Copyright 2006
ALMA MATER STUDIORUM - Università  di Bologna
Via Zamboni, 33 - I-40126 Bologna