INTRODUCTION
There exist different degrees of approximation to describe the diffusion of photons. The first stage, and more widely known, is a scalar model which considers a photon which does not modify its polarisation state. Under this description, photons behave as neutral particles and the transport description is analogous to that of neutrons. The photon interactions are described using average polarised differential cross-sections. This approach is customarily used to study the diffusion of unpolarised photons, in a first approximation (Fernández and Molinari, 1991). A deepest level of detail is reached by including the polarisation state of the photon into the transport equation. This is done with recourse to the so called vector transport equation which describes the transport of photons starting with an arbitrary polarisation state (Chandrasekhar, 1950; Fano, Spencer and Berger, 1959; Pomraning, 1973; Fernández, Hubbell, Hanson and Spencer, 1993). The wave nature of the photon flux is fully represented by the polarisation state, whose evolution is described by the vector equation. The vector equation provides a more complete picture of the photon physics during the diffusion process which allows the treatment of a number of scattering problems closely related to the polarisation state of the source. In what follows, the scalar and vector models of photon diffusion will be formulated and solved for a simple physical model which resembles an infinite thickness target irradiated with collimated and monochromatic x-rays.
The solution to the Boltzmann vector equation gives the possibility of analysing different aspects of the emitted x-ray spectra, from the spectral intensity distribution as a function of energy, to the modification of the polarisation state along the collisions that the photons undergone into the sample. It leads to a very precise knowledge of the emitted spectrum which cannot be reached by solving the more simple scalar equation. In alternative to the analytical solution of the equation, a special vector Monte Carlo code has been used (Fernández, Bastiano and Tartari, 1998) to estimate those higher order of collisions which are not reachable in practice with analytical techniques. It is worth to note the limited capability to describe appropriately the x-ray spectrum of the Monte Carlo codes which use scalar approaches (Fernández, 1998).
To study the multiple scattering of photons means to study the chains of collisions that mix the effects of the different interactions which are possible at the energy regime considered. In this sense, no interaction can be considered separately without taking also into account the other accompanying interactions.
One of the relevant results observed during the formulation of the vector transport equation is the partial coverage of the wave properties of the photons with this model. In fact, even if the vector equation is an important step forward for the description of radiative transfer with respect to the scalar approach used to describe “particle”-like photons, it is still insufficient to provide a whole description of an important phase-related property like coherence. In this sense, the vector equation seems to be appropriate for describing photon beams which add incoherently among them, but not for describing coherent interference. In the frame of radar waves transport, coherence has been described independently to the transport equation, given as a additive term to the vector solution for diffuse incoherent radiation (Mishchenko, 1996). Clearly, such a treatment cannot describe the exchange between the coherent and incoherent states during the diffusion, limiting the validity of the approach to situations where coherence is not a dominant effect. It cannot be applied to describe the transport of coherent x-ray sources, for instance. New approaches are being investigated in order to include the concept of coherence into the vector transport equation. In this page, it will be considered the present state of the treatment of coherence in x-ray spectra.
MATHEMATICAL DESCRIPTION OF PHOTON DIFFUSION
The flow of x-rays is completely determined as the solution of a transport equation describing the balance between the number of photons of given energy and direction entering and leaving an infinitesimal volume element. This balance may be formulated for conditions where the x-ray source is constant in time (steady-state problem) and, therefore, also the photon flow in the medium.
In what follows we shall first show the scalar integro-differential Boltzmann transport equation for photons for a simple model of backscattering from an infinite thickness target, second, show the vector equation necessary to describe the evolution of the polarisation state of the interacting radiation after the collisions, and third, discuss the differences between the two equations. The selected model assumes that photons only interact in the target, i.e. the photons escaping towards the empty half-space may suffer absorption but cannot be sent back to the target. This model represents fairly well the behaviour of radiation in two media of different density (the density in the sample being much greater than the density in the surrounding empty space or air).
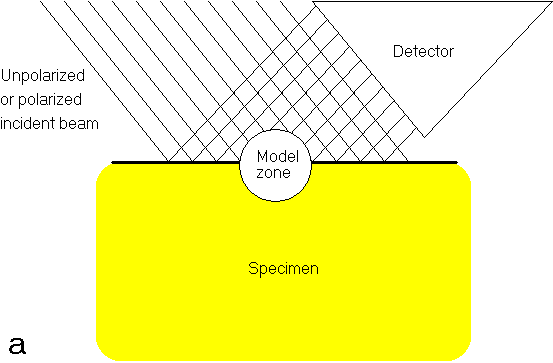
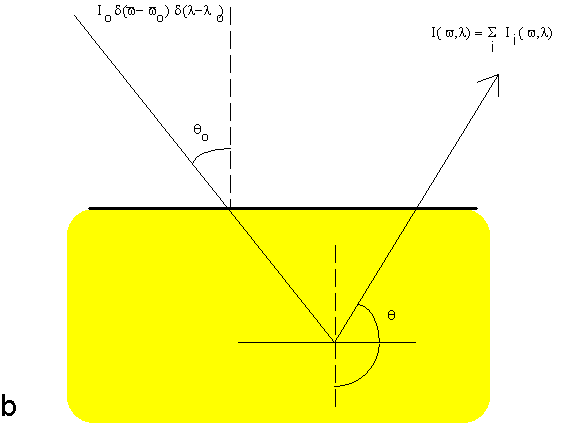
Figure 1. Two schemes for the back-scattering model. (a) Reflection set-up in x-ray spectrometry showing the excitation with a collimated x-ray beam and collimated detection. The circle denotes the zone of applicability of the model. (b) The photon transport equation is solved for a slant monochromatic beam of unpolarised or polarised x-ray photons.
The scalar Boltzmann equation for the above model is
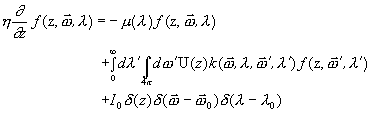(1)
where
denotes the directional cosine
,
the differential of solid angle in the direction of the unitary vector
and
the unitary step Heaviside function. Let us consider a point
and an infinitesimal right cylinder with a base area dA centred at
and with a height dl, whose lateral surface is parallel to a direction
. We define the flux
as the number of photons with wavelengths between
and
, and with directions between
and
, which cross a unit area of the base of the infinitesimal cylinder per unit time. In Eqn (1),
is the specimen's total mass attenuation coefficient,
the probability density function of photon scattering into
from
(per unit path through the medium and per unit
and
), and
represents a plane slant source of
uniformly distributed
producing an incident beam of parallel rays with flight direction
and wavelength
, hitting the infinite sample surface at z=0. It should be noted that, although the scalar transport Eqn (1) is one-dimensional in the space coordinates, the flux maintains all the angular information through its dependence on
. According with the model, the empty semi-space in Eqn (1) is figured through its non-restitution property, rather than by a change in the density or in the absorption coefficient. This choice allows us to use
independent from
in the transport equation.
An analytical (orders of interactions) solution for Eqn (1) is possible (Fernandez and Molinari, 1991), which is obtained by computing separately the contributions after one, two, etc. collisions
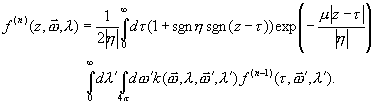(2)
The source term required to start the recursive computation in Eqn (2) is given by
(3)
Finally, the complete albedo solution for the intensity (i.e., the intensity just on the surface of the sample) can be written as
(4)
 |
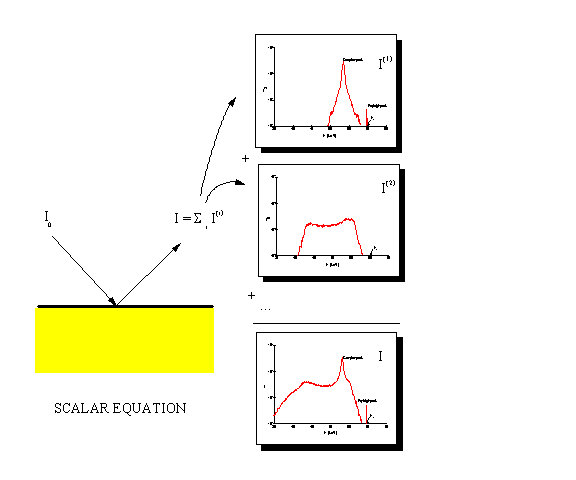Figure 2. Schematic representation of the orders-of-interaction solution obtained with the scalar equation. Each number of collisions contributes a spectral term to the overall spectrum. Every term can be split again into the contributions involving different collision chains of the participating interactions.
|
Representation of polarised radiation with the Stokes parameters
The polarisation of x-rays, a net wave effect, needs four parameters to be represented. The intensity of the beam is the only parameter considered in scalar transport models. At each space point and for a given wavelength and direction of propagation, the most general beam of x-rays can be regarded as a mixture of elliptically polarised and unpolarised x-rays. The fraction of polarised x-rays (the degree of polarisation) is the second parameter. The remaining two parameters are necessary to describe the ellipse associated with the elliptically polarised component. One specifies the angle between the major axis of the ellipse and a fixed coordinate axis in the space. This is generally referred to as the orientation of the ellipse of polarisation. The other is the ellipticity of the ellipse, i.e., the ratio of the two axes of the ellipse. Because of the diverse nature of these four quantities, it is convenient to use an equivalent set, introduced by Sir George Stokes (1852), which contains all the physical information about the polarisation state of the x-ray beam. In this way, the photon transport can be described using a four-component parameterisation obeying a vector transport equation. In this representation, a polarised beam of x-rays needs four parameters
(the Stokes parameters, having the dimension of an intensity) to specify the intensity, the degree of polarisation, the orientation and the ellipticity of the ellipse of polarisation, at each point of the space and in any given direction.
 |
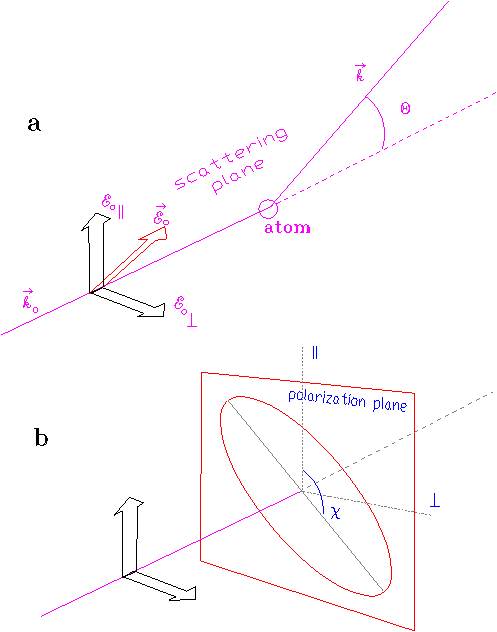Figure 3. Graphical representation of the electric field vector of a polarised photon beam. (a) The scattering geometry determines the scattering plane, used as a reference frame. The electric field can be resolved in the parallel and normal directions to this plane. (b) The electric field vector lies on the polarisation plane, which is normal to the propagation direction. The most general pure state of polarisation of the photon beam is elliptical polarisation. This means that the tip of the electric vector describes an ellipse on the polarisation plane during the propagation. A linearly polarised beam is obtained as a limiting case by making zero the length of the minor axis of the ellipse. In that case, the angle c represents the orientation of the line along which the electric field changes its amplitude periodically.
We can express the Stokes intensities in terms of the angles c (rotation of the major axis of the polarisation ellipse about a direction parallel to the scattering plane) and b (related to the major-to-minor axes ratio or ellipticity). The meaning of these parameters become apparent from the relationships:
(5)
(6)
(7)
The Stokes components for an unpolarised beam are simply
. For elliptically polarised x-rays we note that
(8)
(9)
and the Stokes parameters verify the relation
(10)
Consequently, only three of the four parameters are independent.
For partially polarised x-rays (i.e. a mixture of unpolarised and elliptically polarised x-rays), all the four parameters are necessary and the following relation holds
(11)
Clearly the total intensity
and the additional parameters
, completely determine, from an experimental point of view, the characteristics of an arbitrary beam. That is, two beams with the same Stokes parameters, are optically equivalent since experimentally they cannot be distinguished.
A general beam of x-rays (with components
) can be decomposed into two independent beams, one unpolarised and the other elliptically polarised, with their states of polarisation defined by
(unpolarised) (12)
(elliptically polarised) (13)
where b and c are given by the relationships
(14)
(15)
It is customary to define the degree of polarisation P as the fraction of polarised (scattered) radiation after the collision, which in terms of the Stokes intensities is given by
(16)
It can be easily shown that the general beam can be written as
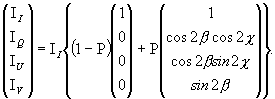(17)
|
So far, the scalar Eqn (1) has not included rigorously the state of polarisation in the description of the radiation field. However, in some cases polarisation can be taken into account in the scalar kernels by defining appropriately the interactions between photons and matter. For instance, it is current practice to consider scattering kernels for unpolarised radiation depending on an average state of polarisation. This choice gives valid results for the first collision of the incident radiation (assuming a polarisation-insensitive detector). However, the subsequent collisions have wrong intensities, as has been shown (Fernández et al., 1993), because the equation is not able to describe the polarisation acquired or lost through the undergone scattering collisions.
The transport equation describing formally the vector flux
of polarised photons in the Stokes system (having components
and
) for the same backscattering framework considered previously can be written as
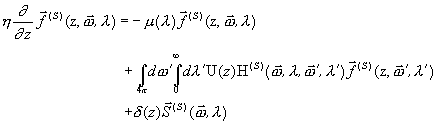(18)
where
(19)
is the kernel matrix in the meridian plane of reference;
the scattering matrix in the scattering plane of reference; and
the four-by-four rotation matrix which transforms the scattered flux from the scattering plane to the meridian plane of the reference. Primed magnitudes denote incidence.
is the narrow-beam attenuation coefficient which is independent of the state of polarisation of the photons (assuming the matter is isotropic), and
the source vector flux with components
. The rotation angles
and
in Eqn (19) are defined by the relationships
(20)
and
(21)
where
and
are the cosines of the polar angles in spherical geometry, and
and
the azimuthal angles. For an axis rotation through an angle
in the clockwise direction, the matrix
is defined as
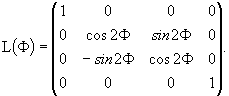(22)
Equation (18) represents a system of four integro-differential equations
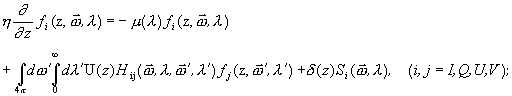(23)
where
denotes the corresponding matrix element of
. It is worth noting that the interaction term introduces coupling between the components of the angular flux as long as
is non diagonal.
The solution of the proposed model can be carried out through an orders-of-interaction solution (Fernández et al., 1993),
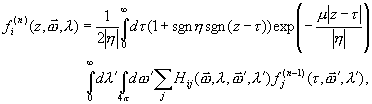(24)
with source function
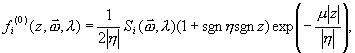(25)
and with (i,j = I,Q,U,V). The whole intensity is obtained (component by component) by adding the contributions from the different number of collisions, similarly as for the scalar model
(26)
 |
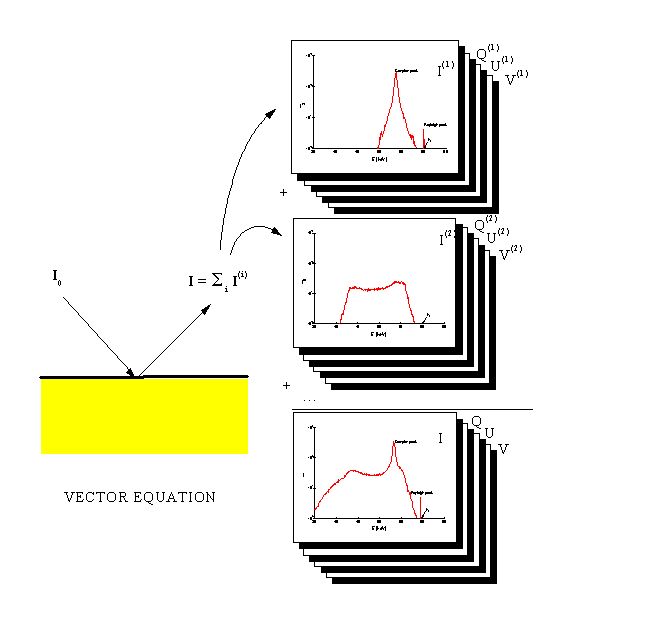Figure 4. Schematic representation of the orders-of-interaction solution obtained with the vector equation. Each number of collisions contributes a term to the overall spectrum. All the terms are formed by the four components of the Stokes intensity. This makes possible to determine the contribute of every term to the state of polarisation of the spectrum as a function of the energy. Every term can be split again into the contributions involving different collision chains of the participating interactions.
|
Differences and similarities between the scalar and the vector model
From a mathematical point of view, the only apparent difference between Eqn (18) and the scalar equation for average polarised radiation, Eqn (1), is the vector character of Eqn (18). The similarity between both equations for an incoherent source is more deep because both represent linear equations, which ensures that an overlap of source terms will produce a corresponding overlap of solutions. This strong property supports the idea of computing orders-of-interaction solutions for both equations.
The new ideas introduced by Eqn (18) are many and are responsible for substantial differences between the solutions of both equations.
First, we obtain the four coupled equations (23) which give, respectively, the Stokes components of the intensity. These components are a means to determine how the state of polarisation changes after every collision, and therefore they give richer information about the whole transport process. The first Stokes component represents the detected intensity, and corresponds to the solution of the scalar equation. Although the vector equation is linear, the single equation for the intensity is non-linear due to the coupling terms. This fact has two important consequences. In first place, it is not possible to solve separately the equation for the intensity without considering the other coupled equations. This prevents against looking for a solution for this single scalar equation, without considering the evolution of the full polarisation state (even using a Monte Carlo). In second place, the solution obtained for the intensity is different from the one predicted with the scalar equation for unpolarised excitation, except for the first collision that gives the same result in both cases. For polarised excitation the intensity has been calculated using the whole vector equation, and therefore a direct comparison with solutions of some scalar equation using polarisation-dependent kernels has been not possible. However, it was shown that for the case of linear polarisation it is not possible to establish a parallelism between both types of solutions, scalar and vector, since the coupling of the flux components in Eqn (18) produces only new states of linear polarisation for scattering collisions (with electrons having randomly oriented spins, i.e. for non-magnetic states of the matter). This allows us to hypothesise that Monte Carlo programs (Namito et al., 1993; Vincze et al., 1993) using scalar (but polarisation-dependent) differential cross-sections, will never produce equivalent results to the vector solution because they cannot describe appropriately (i.e. at every collision) the exchange between polarised and unpolarised states produced by the scattering events. A formal demonstration of such impossibility has been given by Fernandez (1998).
For matter under an external magnetic field, the Compton matrix kernel has non-zero matrix components (Fano, 1949) in the last row and column that create non-linear components of polarisation in each collision. This condition prevents the use of a scalar model of transport. Besides the well known magnetic behaviour of Compton scattering, a similar behaviour for Rayleigh scattering has also been reported (Simon and Daniel, 1977). For non-linear polarisation of the incidence beam (circular polarisation for instance), the requirement is similar to that for the linear polarisation case. In the absence of an external magnetic field the last equation in Eqn (23) [corresponding to
] is not coupled, and the vector equation can be reduced of one dimension. For a magnetic field, in contrast, it is mandatory to use the full vector model of transport.
Second, the fact that the rotations that appear in Eqn (19) modify the angular dependence of the kernel
, is very important. Indeed, the kernel
in the local-center-of-mass system, due to the symmetry of the collision, depends on the scattering angle but not on the incidence direction. This is a very intuitive result that can be easily verified on all the scattering processes in the x-ray regime. Mathematically, this means that the kernel will depend on the scalar product
and not on the directions
or
individually. This property can be understood as a consequence of the isotropy of the space in which the collision undergoes. However, the kernel
appearing in the transport Eqn (18), is the kernel
after the two rotations shown in Eqn (19). These rotations destroy the kernel dependence on
, and make it dependent on
and
separately. In other words, these rotations destroy the isotropy of the space and make the angular distribution produced as a consequence of the scattering processes appear deformed with respect to the original distribution in the local-centre-of-mass system. An example of this property is shown in Fig. 5.
 |
 |
 |
Figure 5. Isointensity surfaces illustrating the angular dependence of the first order intensity of Rayleigh scattering for unpolarised and linearly polarised sources with different orientations of the electric vector: (a) unpolarised beam (intensity shows azimuthal symmetry around the incidence direction), (b) linearly polarised on the plane x-z (intensity is null for the scattering direction, and maximum on a normal plane to it), (c) linearly polarised along y (intensity is maximum on the plane x-z, and null on the y axis).
The last consideration concerns the influence of polarisation on the different types of interactions in the x-ray regime. The Rayleigh and Compton scattering processes are strongly dependent on the polarisation, while the transitions that fill photoelectric vacancies are almost independent of it. Multiple collisions will mix the effects of the polarisation on the single participating collisions. In this way, multiple collisions involving the photoelectric effect preceded by a scattering collision will bring the effect of the polarisation also on the characteristic lines. Under these circumstances, there is no one part of the x-ray spectrum that remains completely independent of the state of polarisation of the source.
|
References
Chandrasekhar S (1950) Radiative Transfer Clarendon Press, Oxford [(1960) Reprinted with corrections by Dover, New York]. Ch.1 (The Equations of Transfer), particularly Sec. 15 (The Representation of Polarised Light).Cohen DD (1987) Average L shell fluorescence yields. Nucl. Intrum. Methods B22, 55.
Fano U (1949) Remarks on the Classical and Quantum-Mechanical Treatment of Partial Polarization. J. Opt. Soc. Am.39, 859-863.
Fano U, Spencer LV and Berger MJ (1959) Penetration and diffusion of X-rays. In Encyclopedia of Physics, Vol 38/2, p. 660. Springer Verlag, Berlin.
Fernández JE (1998) Non-linear effects in polarised photon transport. Appl.Rad Isot.49, 83.
Fernández JE and Molinari VG (1990) Theoretical estimation of the fourth-order XRF intensity. Adv. X-Ray Anal.33, 573-580.
Fernández JE and Molinari VG (1991) X-Ray Photon spectroscopy calculations. In: Advances in Nuclear Science and Technology, Vol. 22, J Lewins, M Becker eds., Plenum Press, New York, pp. 45-104.
Fernández JE, Bastiano M and Tartari A (1998) Vector Monte Carlo for simulation of polarized photons. X-Ray Spectrometry 27, 325-331.
Fernández JE, Hubbell JH, Hanson AL and Spencer LV (1993) Polarization effects on multiple scattering gamma transport. Rad. Phys. Chem.41, 579-630.
Mishchenko MI (1996) Diffuse and coherent backscattering by discrete random media--I. Radar reflectivity, polarisation ratios, and enhancement factors for a half-space of polydisperse, nonabsorbing and absorbing spherical particles. Journal of Quantitative Spectroscopy & Radiative Transfer 56, 673-702
Namito Y, Ban S and Hirayama H (1993) Implementation of linearly-polarized photon scattering into the EGS4 code. Nucl. Instr. Meth. Phys. Res.A332, 277-283.
Pomraning GC (1973) The equations of radiation hydrodynamics, Pergamon Press, Oxford.
Simon T and Daniel H (1977) Measurement of the Spin Dependence of Rayleigh Scattering. Phys. Rev.A15, 1015-1022.
Vincze L, Janssens K, Adams F (1993) A general Monte Carlo simulation of ED-XRF spectrometers. Part I: Unpolarized radiation, homogeneous samples. Spectrochim. ActaB48, 553-573
|
